Textures

We have seen how to fill a closed curve with a solid colour using the FillColour attribute. The Texture attribute lets you specify a fill colour parameterised by a pixel coordinate and a texture coordinate. The texture coordinate is given relative to a customizable texture basis.

> import Graphics.Curves
> import Data.NumInstances

Using texture coordinates

First, let's have ourselves an invisible egg

> egg = curve 0 (2 * pi) (\t ->
>           Vec (0.8 * cos t * (1 - 0.12 * sin t))
>               (0.95 * sin t))
>         `with` [ LineColour := transparent ]

The rest of this page is dedicated to giving the egg pretty colours, but for reference, this is what it looks like with the LineColour turned back on.

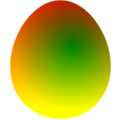
Let's have a red texture which is darker closer to the center of the egg and a green texture that grows darker towards the bottom. Adding 1 them together produces a pretty yellow egg.

> redTex   _ p = Colour (distance p 0) 0 0 1
> greenTex _ p = Colour 0 (0.5 + 0.5 * getY p) 0 1
>
> redEgg    = egg `with` [ Texture := redTex   ]
> greenEgg  = egg `with` [ Texture := greenTex ]
> yellowEgg = egg `with` [ Texture := redTex + greenTex ]
>
> eggs = redEgg <> translate (Vec 2 0) greenEgg
>               <> translate (Vec 4 0) yellowEgg

Texture coordinates are transformed together with the image, so the texture sticks with an object when it's transformed as you would expect.

> tilt = rotate (pi/4) yellowEgg

The texture basis

Texture coordinates are given in a customizable coordinate system defined by the TextureBasis attribute of the image. A Basis consists of three points, (origin, xUnit, and yUnit) and describes a coordinate system with origin origin and basis vectors xUnit - origin and yUnit - origin The texture coordinate of a point p is Vec s t, where

>   p == diag s * (xUnit - origin) + diag t * (yUnit - origin)

In picture form:

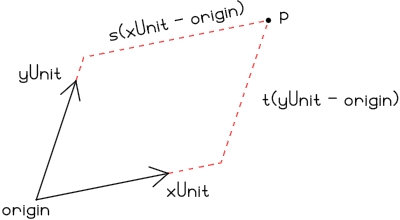The toBasis and fromBasis functions lets you convert between points in the defaultBasis and an arbitrary basis.

With the theory out of the way, let's mess with the egg. Modifying the texture basis in effect applies the corresponding transformation to the texture. For instance, we can turn the egg texture upside down and move it slightly off-center as follows:

> upsideDown = yellowEgg `with`
>   [ TextureBasis :~ translate 0.2 . rotate pi ]

When an image is transformed, the texture basis is also transformed 2. This is true even if we haven't set a texture for the object, which can lead to slightly surprising behaviour in cases. Compare the two balls below

> scaled = (ball1 2 <> translate (Vec 4.3 0) ball2 2)
>           `with` [ Texture    := redTex + greenTex
>                  , LineColour := transparent ]
>   where
>     ball1 r = curve 0 (2 * pi) $ \t -> Vec (r * cos t) (r * sin t)
>     ball2 r = scale r (ball1 1)

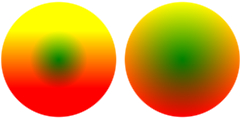The left ball is drawn as a circle with radius two using curve, and the the right ball is a circle with radius one scaled by a factor of two. The difference between the two is that the the left ball has the default texture basis and the right one a scaled-up basis. Of course, you can always reset the texture basis of an object if it isn't what you want.

> scaled' = scaled `with` [ TextureBasis := newBasis ]
>   where
>     newBasis = translate (Vec 2.15 0) $ scale 3 defaultBasis

Using pixel coordinates

Unlike the texture coordinates, pixel coordinates are completely unaffected by image transformations. The value of the pixel coordinate is always the position of the pixel being coloured in the final PNG image. One use case for pixel coordinates is to create raster effects like these:

> chessEgg = egg `with` [ Texture := \(Vec x y) _ ->
>                           if even (floor (x / 10) + floor (y / 10))
>                           then Colour 1   0 0 1
>                           else Colour 0.5 0 0 1 ]

As advertised, transforming the chess egg does nothing to the texture.

> chessEggs = chessEgg <> translate (Vec 1 0) (rotate (-pi/4) chessEgg)

Of course, that we cannot affect the pixel coordinates with transformations doesn't mean that we can't play around with the texture function itself.

> swirlyEgg = chessEgg `with`
>   [ Texture :~ \tex p q -> tex (rotateAround 60 (2 * distance q 0) p) q ]

Here we used the texture coordinate to change which pixel we sample from the old, pixel-based, texture.

FillColour and Texture interaction

The FillColour and Texture attributes map to the same underlying property. In fact setting the fill colour is (almost 3) equivalent to setting the texture to a constant function. This means that you can change the texture of an image by modifying the fill colour.

> purpleEgg = yellowEgg `with`
>         [ FillColour :~ \(Colour r g b a) -> Colour g b r a ]

▲ 1 Thanks to Conal Elliott's nifty NumInstances package.

▲ 2 This is what lets the texture stay with an object when it is transformed.

▲ 3 The only difference is that if the fill colour is set to transparent, the fill blur is not taken into account when computing the bounds of an image. Of course, if the texture attribute is set we can't decide 4 if it's the constant transparent function.

▲ 4 Well I guess we could, since there are a finite 5 number of texture function inputs. It would just take a while.

▲ 5 115792089237316195423570985008687907853269984665640564039457584007913129639936 to be precise. curves-1.1.0.1: Ulf Norell <ulf.norell@gmail.com>Sat Oct 18 09:12:49 EEST 2014